理解 AVL 树
理解 AVL 树
参考资料:强烈推荐通过 visualgo 中的例子来感受 AVL 树在各种操作下的再平衡过程。二叉树的再平衡的过程非常解压
树结构的代码天然适合递归的写法。
基本了解
首先我们要了解二叉搜索树(BST, Binary Search Tree)
- 定义:对任意节点来说,左子树所有节点值小于当前节点值,右子树所有节点值大于当前节点值。
- 特点:适用于快速查找和有序遍历。
AVL 树:最早的自平衡 BST,严格保证平衡因子(左右子树高度差)不超过 1。
其实我们用一个树节点就可以代表一个树
public class AVLTreeNode {
int value;
AVLTreeNode left, right;
}
其实乍一看,树跟链表这种结构起始没什么区别,在链表中,只要有链表的头节点,我们就能最对这个链表进行增删改查,
二叉树也是如此,我们只要知道树的根节点就可以遍历整个树,
但是为了实现 左子树所有节点值小于当前节点值,右子树所有节点值大于当前节点值。和 左右子树高度差不超过 1,我们要做很多操作。
AVL 树的代码
AVL 树节点 MyAVLTreeNode,这里为了方便打印其结构,实现了 BTPrinterAdapter,具体请看 在控制台输出二叉树的结构
public class MyAVLTreeNode<K extends Comparable<K>, V> implements BTPrinterAdapter<MyAVLTreeNode<K, V>> {
public K key;
public V val;
// 用于评估平衡度,每次都通过递归的方式去算太耗时,直接用一个字段保存,然后每一级递归的时候更新,这样会快很多
public int height;
public MyAVLTreeNode<K, V> left, right;
public MyAVLTreeNode(K key, V val) {
this.key = key;
this.val = val;
this.height = 1;
this.left = null;
this.right = null;
}
@Override
public String getNodeString() {
return key.toString() + ":" + val.toString();
}
@Override
public MyAVLTreeNode<K, V> getLeftNode() {
return left;
}
@Override
public MyAVLTreeNode<K, V> getRightNode() {
return right;
}
}
AVL 树本身 MyAVLTree
public class MyAVLTree<K extends Comparable<K>, V> {
private MyAVLTreeNode<K, V> root;
public MyAVLTreeNode<K, V> search(K key) {
if (root == null) {
return null;
}
MyAVLTreeNode<K, V> target = null;
MyAVLTreeNode<K, V> nowRoot = root;
// 其实也可以写成递归,但是没必要,就用 for 循环就够了
while (nowRoot != null) {
int flag = key.compareTo(nowRoot.key);
if (flag == 0) {
target = nowRoot;
break;
}else if (flag < 0) {
// 从左子树往下找
nowRoot = nowRoot.left;
} else if (key.compareTo(nowRoot.key) > 0) {
// 从右子树往下找
nowRoot = nowRoot.right;
}
}
return target;
}
public MyAVLTreeNode<K, V> insert(K key, V value) {
if (key != null && value != null) {
// 需要更新根节点
root = insert(root, key, value);
}
return root;
}
public MyAVLTreeNode<K, V> insert(MyAVLTreeNode<K, V> nowRoot, K key, V value) {
if (nowRoot == null) {
return new MyAVLTreeNode(key, value);
}
int compare = key.compareTo(nowRoot.key);
if (compare < 0) {
nowRoot.left = insert(nowRoot.left, key, value);
} else if (compare > 0) {
nowRoot.right = insert(nowRoot.right, key, value);
} else {
nowRoot.val = value;
return nowRoot;
}
// 更新树高
nowRoot.height = getHeightFromLeftAndRight(nowRoot);
// 查看平衡度
int balance = getBalance(nowRoot);
// 根据平衡度来调整树
nowRoot = reBalance(nowRoot, balance);
return nowRoot;
}
// 删除节点,
public MyAVLTreeNode<K, V> delete(K key) {
if (key != null) {
root = delete(root, key);
}
return root;
}
public MyAVLTreeNode<K, V> delete(MyAVLTreeNode<K, V> nowRoot, K key) {
if (nowRoot == null) {
return null;
}
int compare = key.compareTo(nowRoot.key);
if (compare < 0) {
nowRoot.left = delete(nowRoot.left, key);
} else if (compare > 0) {
nowRoot.right = delete(nowRoot.right, key);
} else {
// nowRoot 就是要删除的节点
if (nowRoot.left == null && nowRoot.right == null) {
// 如果这个节点没有子节点,则直接删除就行了
// 直接返回 null 表示删除当前节点
return null;
} else if (nowRoot.left != null && nowRoot.right == null) {
// 如果左不为空,右为空,左节点直接向上替代
return nowRoot.left;
} else if (nowRoot.right != null && nowRoot.left == null) {
// 如果右不为空,左为空,右节点直接向上替代
return nowRoot.right;
} else {
// 二者都不为空
// 从右节点找出最小的把 key 和 value 替换过来
MyAVLTreeNode<K, V> minNode = findMinNode(nowRoot.right);
nowRoot.val = minNode.val;
nowRoot.key = minNode.key;
// 因为 minNode 没有子节点,所以,删除 minNode 的时候不会再次进入这个循环
nowRoot.right = delete(nowRoot.right, minNode.key);
}
}
nowRoot.height = getHeightFromLeftAndRight(nowRoot);
int balance = getBalance(nowRoot);
nowRoot = reBalance(nowRoot, balance);
return nowRoot;
}
private int getHeight(MyAVLTreeNode<K, V> root) {
return root == null ? 0 : root.height;
}
private int getHeightFromLeftAndRight(MyAVLTreeNode<K, V> root) {
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
private int getBalance(MyAVLTreeNode<K, V> root) {
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return leftHeight - rightHeight;
}
private enum BalanceType {
LL,
LR,
RR,
RL
}
/**
* 核心方法,AVL 树再平衡
*/
private MyAVLTreeNode<K, V> reBalance(MyAVLTreeNode<K, V> nowRoot, int balance) {
if (balance < -1 || balance > 1) {
BalanceType type = null;
if (balance > 1) {
// 因为左边树高至少是 2,所以 nowRoot.left 一定是不为 null 的
int leftBalance = getBalance(nowRoot.left);
if (leftBalance < 0) {
// 需要旋转两次
type = BalanceType.LR;
} else {
// 只用旋转一次
type = BalanceType.LL;
}
} else if (balance < -1) {
int rightBalance = getBalance(nowRoot.right);
if (rightBalance > 0) {
// 需要旋转两次
type = BalanceType.RL;
} else {
// 只用旋转一次
type = BalanceType.RR;
}
}
if (type != null) {
switch (type) {
case LL:
return rightRotate(nowRoot);
case LR:
// 旋转之后,需要将旋转后的结果更新到原来的树上
nowRoot.left = leftRotate(nowRoot.left);
return rightRotate(nowRoot);
case RR:
return leftRotate(nowRoot);
case RL:
// 旋转之后,需要将旋转后的结果更新到原来的树上
nowRoot.right = rightRotate(nowRoot.right);
return leftRotate(nowRoot);
}
}
}
return nowRoot;
}
// 始终记住三个参数的关系,即 y > T2 > x 这样写左旋或者右旋就不会乱
// 我们修改也就是这三个节点,更新的也只有这三个节点
private MyAVLTreeNode<K, V> rightRotate(MyAVLTreeNode<K, V> y) {
MyAVLTreeNode<K, V> x = y.left;
MyAVLTreeNode<K, V> T2 = x.right;
x.right = y;
y.left = T2;
// 这里我们只用更新 x 和 y 的树高,为什么,因为我们并没有修改 T2 的左右子节点
// 更新 height 的时候,一定要注意,要先更新下级节点的高度,再更新上级节点的高度,因为上级节点的高度取决于下级节点的高度
y.height = getHeightFromLeftAndRight(y);
x.height = getHeightFromLeftAndRight(x);
return x;
}
private MyAVLTreeNode<K, V> leftRotate(MyAVLTreeNode<K, V> x) {
MyAVLTreeNode<K, V> y = x.right;
MyAVLTreeNode<K, V> T2 = y.left;
y.left = x;
x.right = T2;
x.height = getHeightFromLeftAndRight(x);
y.height = getHeightFromLeftAndRight(y);
return y;
}
/**
* 查找最小的节点,只用从最左边往下找即可。
*/
public MyAVLTreeNode<K, V> findMinNode(MyAVLTreeNode<K, V> nowRoot) {
if (nowRoot == null) {
return null;
}
MyAVLTreeNode<K, V> minimalNode = nowRoot;
while (nowRoot != null && nowRoot.left != null) {
minimalNode = nowRoot.left;
nowRoot = minimalNode;
}
return minimalNode;
}
public MyAVLTreeNode<K, V> getRoot() {
return root;
}
}
测试代码
public static void main(String[] args) {
MyAVLTree<Integer, String> tree = new MyAVLTree<Integer, String>();
tree.insert(1, "a");
BTPrinter.printTree(tree.getRoot());
tree.insert(2, "b");
BTPrinter.printTree(tree.getRoot());
tree.insert(3, "c");
BTPrinter.printTree(tree.getRoot());
tree.insert(4, "d");
BTPrinter.printTree(tree.getRoot());
tree.insert(5, "e");
BTPrinter.printTree(tree.getRoot());
tree.insert(6, "f");
BTPrinter.printTree(tree.getRoot());
tree.insert(7, "g");
BTPrinter.printTree(tree.getRoot());
tree.insert(-1, "h");
BTPrinter.printTree(tree.getRoot());
tree.insert(-2, "i");
BTPrinter.printTree(tree.getRoot());
tree.insert(-3, "j");
BTPrinter.printTree(tree.getRoot());
tree.insert(-5, "k");
BTPrinter.printTree(tree.getRoot());
tree.insert(-6, "l");
BTPrinter.printTree(tree.getRoot());
tree.insert(-7, "m");
BTPrinter.printTree(tree.getRoot());
tree.insert(-9, "n");
BTPrinter.printTree(tree.getRoot());
tree.insert(-10, "o");
BTPrinter.printTree(tree.getRoot());
tree.insert(-11, "p");
BTPrinter.printTree(tree.getRoot());
System.out.println("---------------delete-----------------");
tree.delete(5);
BTPrinter.printTree(tree.getRoot());
tree.delete(6);
BTPrinter.printTree(tree.getRoot());
tree.delete(4);
BTPrinter.printTree(tree.getRoot());
tree.delete(-9);
BTPrinter.printTree(tree.getRoot());
tree.delete(-1);
BTPrinter.printTree(tree.getRoot());
System.out.println("---------------search-----------------");
MyAVLTreeNode<Integer, String> target = tree.search(-11);
System.out.println(target.key + ":" + target.val);
}
输出
---
1:a
--------
1:a
|_
2:b
-------------
2:b
_| |_
1:a 3:c
------------------
2:b
_| |_
1:a 3:c
|_
4:d
-----------------------
2:b
_| |______
1:a 4:d
_| |_
3:c 5:e
----------------------------
4:d
______| |_
2:b 5:e
_| |_ |_
1:a 3:c 6:f
---------------------------------
4:d
______| |______
2:b 6:f
_| |_ _| |_
1:a 3:c 5:e 7:g
---------------------------------------
4:d
______| |______
2:b 6:f
_| |_ _| |_
1:a 3:c 5:e 7:g
_|
-1:h
---------------------------------------------
4:d
______| |______
2:b 6:f
______| |_ _| |_
-1:h 3:c 5:e 7:g
_| |_
-2:i 1:a
---------------------------------------------------
4:d
________________| |______
-1:h 6:f
_| |______ _| |_
-2:i 2:b 5:e 7:g
_| _| |_
-3:j 1:a 3:c
---------------------------------------------------------
4:d
________________| |______
-1:h 6:f
_______| |______ _| |_
-3:j 2:b 5:e 7:g
_| |_ _| |_
-5:k -2:i 1:a 3:c
---------------------------------------------------------------
-1:h
_______| |________________
-3:j 4:d
_| |_ ______| |______
-5:k -2:i 2:b 6:f
_| _| |_ _| |_
-6:l 1:a 3:c 5:e 7:g
---------------------------------------------------------------------
-1:h
_______| |________________
-3:j 4:d
_______| |_ ______| |______
-6:l -2:i 2:b 6:f
_| |_ _| |_ _| |_
-7:m -5:k 1:a 3:c 5:e 7:g
---------------------------------------------------------------------------
-1:h
___________________| |________________
-6:l 4:d
_| |_______ ______| |______
-7:m -3:j 2:b 6:f
_| _| |_ _| |_ _| |_
-9:n -5:k -2:i 1:a 3:c 5:e 7:g
----------------------------------------------------------------------------------
-1:h
___________________| |________________
-6:l 4:d
_______| |_______ ______| |______
-9:n -3:j 2:b 6:f
_| |_ _| |_ _| |_ _| |_
-10:o -7:m -5:k -2:i 1:a 3:c 5:e 7:g
-----------------------------------------------------------------------------------------
-1:h
___________________| |________________
-6:l 4:d
_______| |_______ ______| |______
-9:n -3:j 2:b 6:f
_| |_ _| |_ _| |_ _| |_
-10:o -7:m -5:k -2:i 1:a 3:c 5:e 7:g
_|
-11:p
---------------delete-----------------
------------------------------------------------------------------------------------
-1:h
___________________| |________________
-6:l 4:d
_______| |_______ ______| |_
-9:n -3:j 2:b 6:f
_| |_ _| |_ _| |_ |_
-10:o -7:m -5:k -2:i 1:a 3:c 7:g
_|
-11:p
-------------------------------------------------------------------------------
-1:h
___________________| |________________
-6:l 4:d
_______| |_______ ______| |_
-9:n -3:j 2:b 7:g
_| |_ _| |_ _| |_
-10:o -7:m -5:k -2:i 1:a 3:c
_|
-11:p
--------------------------------------------------------------------------
-1:h
___________________| |______
-6:l 2:b
_______| |_______ _| |______
-9:n -3:j 1:a 7:g
_| |_ _| |_ _|
-10:o -7:m -5:k -2:i 3:c
_|
-11:p
--------------------------------------------------------------------
-1:h
___________________| |______
-6:l 2:b
_______| |_______ _| |______
-10:o -3:j 1:a 7:g
_| |_ _| |_ _|
-11:p -7:m -5:k -2:i 3:c
--------------------------------------------------------------
1:a
___________________| |______
-6:l 3:c
_______| |_______ _| |_
-10:o -3:j 2:b 7:g
_| |_ _| |_
-11:p -7:m -5:k -2:i
---------------search-----------------
-11:p
非常漂亮的二叉树的结构
假设有一根线竖着从左往右扫这个图形(这个其实就是中序遍历 94. 二叉树的中序遍历),你会发现,碰到的数刚好就是从小到大排序的。这也是二叉搜索树的特性。二叉树的递归遍历#中序遍历(左中右)
编码过程中的注意点
- 当我们更新了左子树或者右子树的时候,更新后的结果一定要赋值回回当前树的左子树的指针或者右子树的指针中
- 当我们对树进行了旋转,也相当于是更新左子树和右子树,也是需要更新回当前树的左子树的指针或者右子树的指针中的
理解二叉树的代码
其实对于二叉树来说,查找的代码是非常简单的,类似于二分查找,真正难以理解的,其实是插入和删除的时候,保证任意节点左右子树高度差不超过 1 的实现过程。
从上面的代码中我们可以看到,实现主要是通过旋转来实现的。
理解查询的代码
类似于二分查找,
- 如果当前节点的 key 与要查找的 key 相同,则直接返回
- 小于当前节点的 key,则让左子节点作为下一轮比较的节点
- 大于当前节点的 key,则让右子节点作为下一轮比较的节点
其实这个过程也可以用递归实现,不过 while 更简单而且容易理解,就用 while 循环算了。
理解插入的过程
往 AVL 树中插入节点的流程是:
- 首先递归到需要插入的位置,创建节点
- 返回并更新当前树的左子树或者右子树
- 更新当前树的根节点的树高
- 计算当前树的根节点的平衡度
- 根据平衡度进行再平衡
- 递归返回到上一层,重复 2-5 步
因为我们是从 root 节点开始往下寻找位置插入的,所以当递归返回的时候,会检查每一级的平衡因子,因此左旋或者右旋的次数,确实会有点多,这也是后面为什么后面会开发出红黑树(请看 理解红黑树),并成为主流
理解删除的过程
从 AVL 树中删除节点的流程是:
- 找到要删除的节点
- 如果这个节点没有子节点,直接删除
- 如果这个节点只有一个子节点,那直接让那个唯一的子节点代替自己
- 如果两个子节点都存在,则
- 从右子节点中找到最小的节点,替代当前节点,为什么要这样?以递增序列的角度看二叉搜索树,我们在序列中删除了一个元素,那么接替他的,应该是紧随其后的元素,根据二叉搜索树的性质,大于根节点的第一个元素,其实是其右子树中的最小的元素,而右子树的最小的元素,其实是其最深的属于左子树的叶子节点。
- 从右子树中删除这个最小节点
- 返回并更新当前树的左子树或者右子树
- 更新当前树的根节点的树高
- 计算当前树的根节点的平衡度
- 根据平衡度进行再平衡
- 递归返回到上一层,重复 2-5 步
可以看到跟插入的时候除了第一步不一样,后面几步都一样,现在我们就来看看 AVL 树的核心操作,再平衡
理解再平衡的过程 - 重点
再平衡的作用是保持左子树跟右子树的高度差不超过 1,
- 首先判断当前节点左右子树的高度差是否大于 1
- 如果是,则需要进一步判断是哪种类型,总共有四种类型,LL、LR、RR、RL、
- 根据类型,对当前子树进行旋转
- 返回旋转之后的根节点并返回。
1. LL 型(左左)
如果插入或者删除之后,左子树 B 的高度比右子树高出 1 以上,而且左子树的左边 C 比右边高,就是 LL 型,需要对 A 进行一次右旋转
A B
/ / \
B => C A
/
C
2. RR 型(右右)
如果插入或者删除之后,右子树 B 的高度比左子树高出 1 以上,而且右子树的右边 C 比左边高,就是 RR 型,需要对 A 进行一次左旋转
A B
\ / \
B => A C
\
C
3. LR 型(左右)
如果插入或者删除之后,左子树 B 的高度比右子树高出 1 以上,而且左子树 B 的右边 C 比左边高,就是 LR 型,需要先对左子树 B 进行一次左旋转,然后再对当前节点 A 进行一次右旋转
A A C
/ / / \
B => 左旋(B) C => 右旋(A) B A
\ /
C B
4. RL 型(右左)
如果插入或者删除之后,右子树 B 的高度比左子树高出 1 以上,而且右子树的左边 C 比右边高,就是 RL 型,需要先对右子树 B 进行一次右旋转,然后再对当前节点 A 进行一次右旋转
A A C
\ \ / \
B => 右旋(B) C => 左旋(A) A B
/ \
C B
实际过程
上面这四种情况,只是概念模型,ABC 除了图中的左右子节点外,也会有别的节点
而且旋转,是节点树的整体位置的变换,而不是两个单独的节点之间的变换,后面我们会看到
具体的过程,强烈推荐通过 visualgo 中的例子来感受 AVL 树在各种操作下的再平衡过程
假设一开始树形,
图 1:
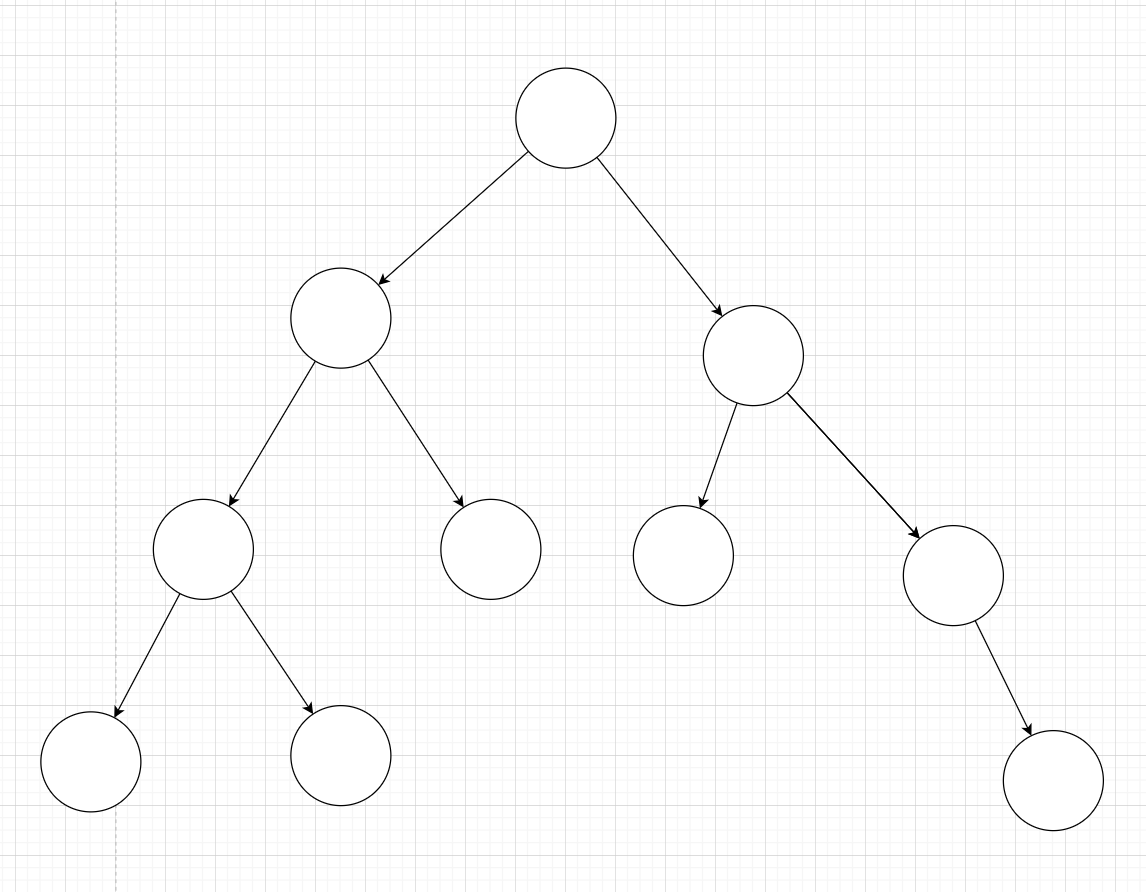
突然加了一个节点,此时 x 是平衡的,但是 y 不平衡
图 2:
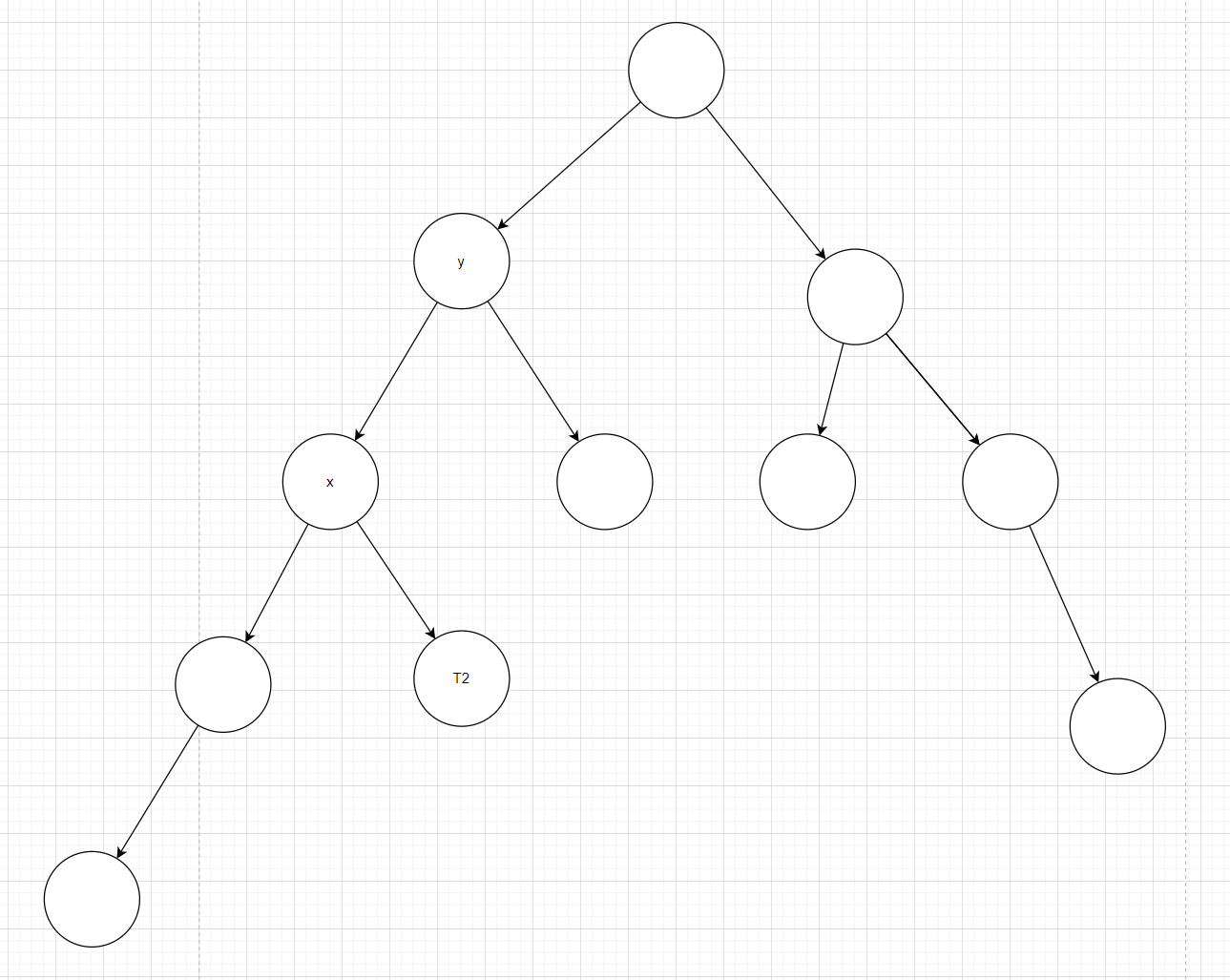
而且此时是 LL,需要一次右旋,结果如下
图 3:
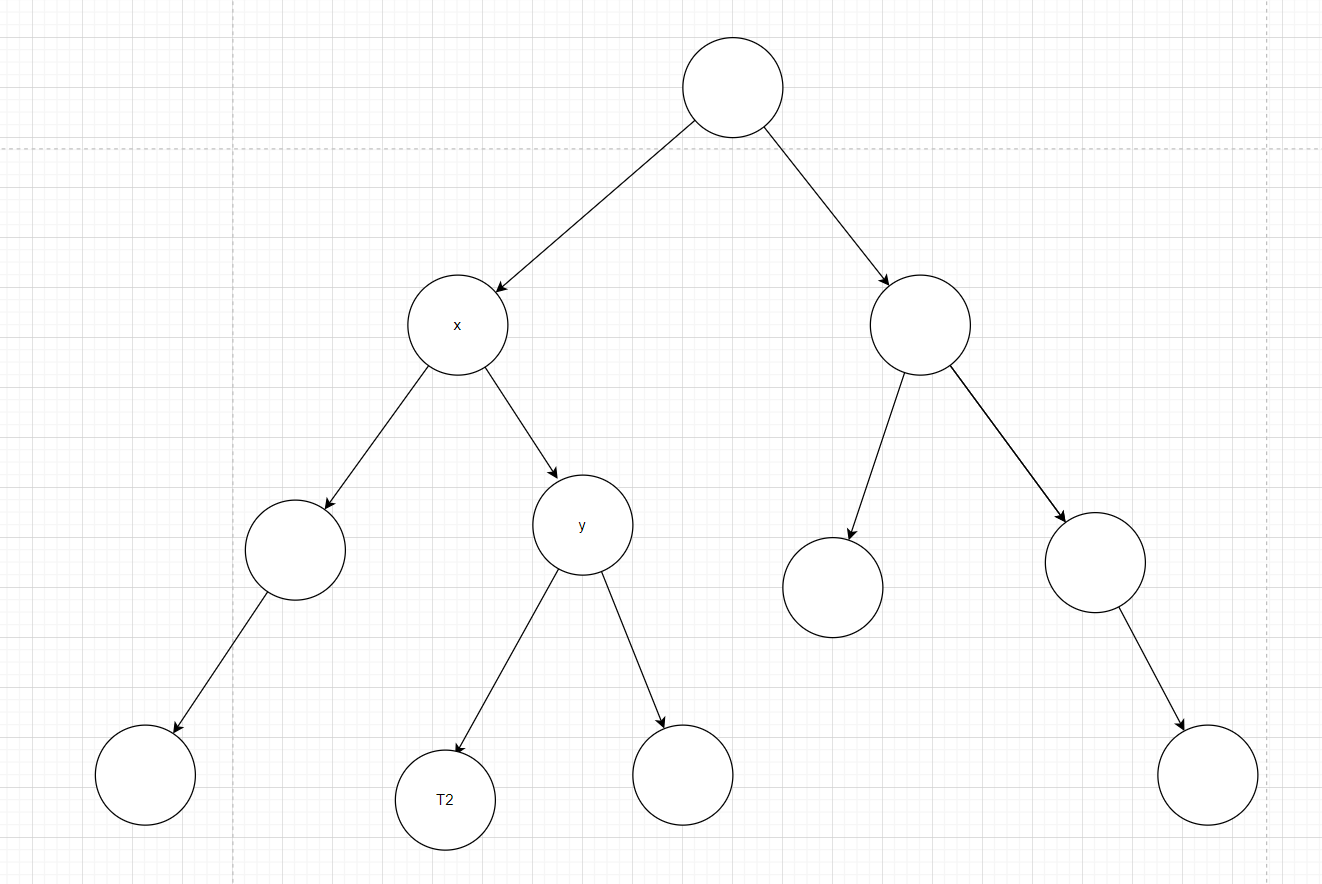
再加一个节点,此时 x 不平衡,此时的状态是 RR,需要一次左旋
图 4:
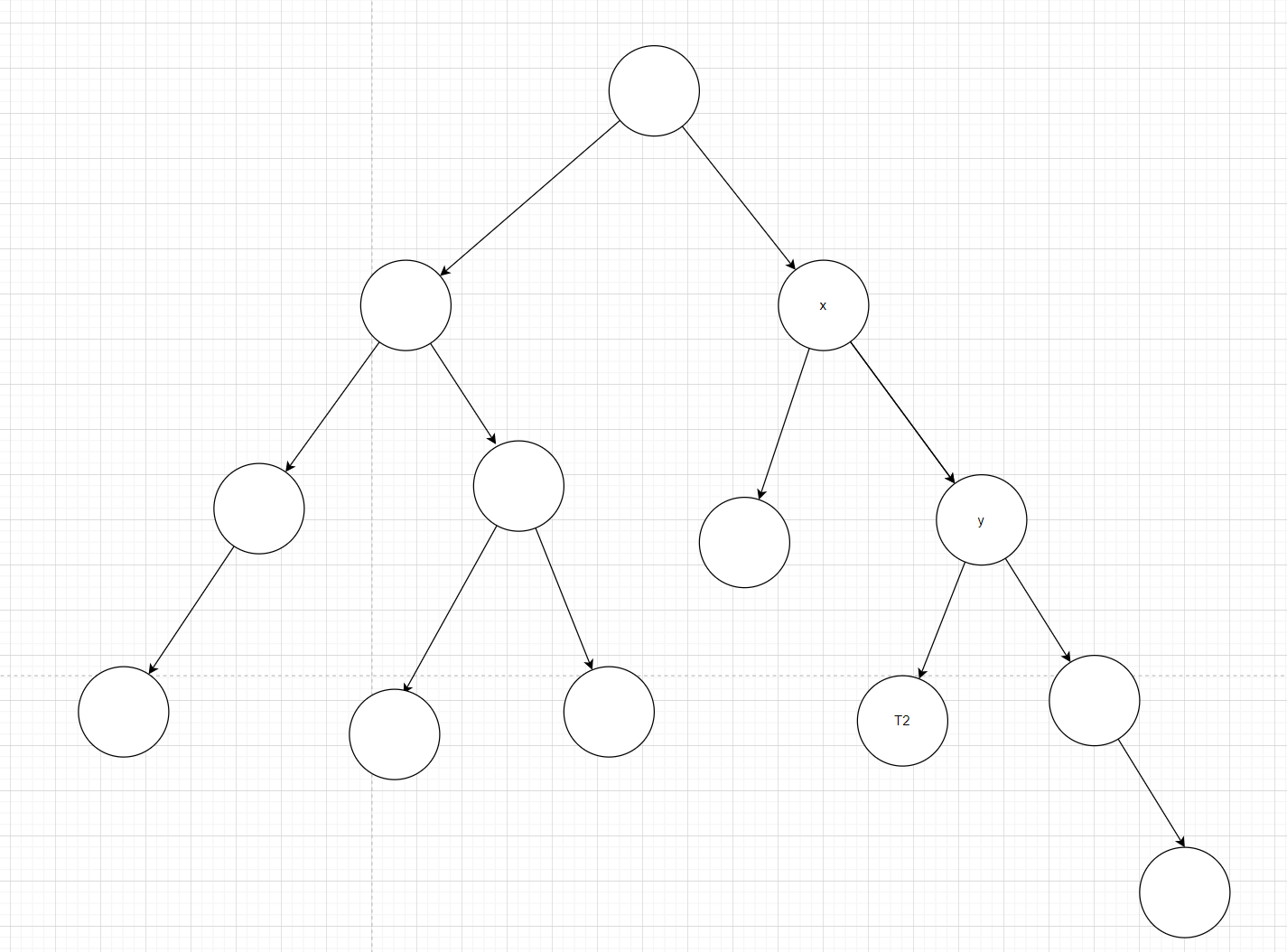
左旋之后的结果
图 5:
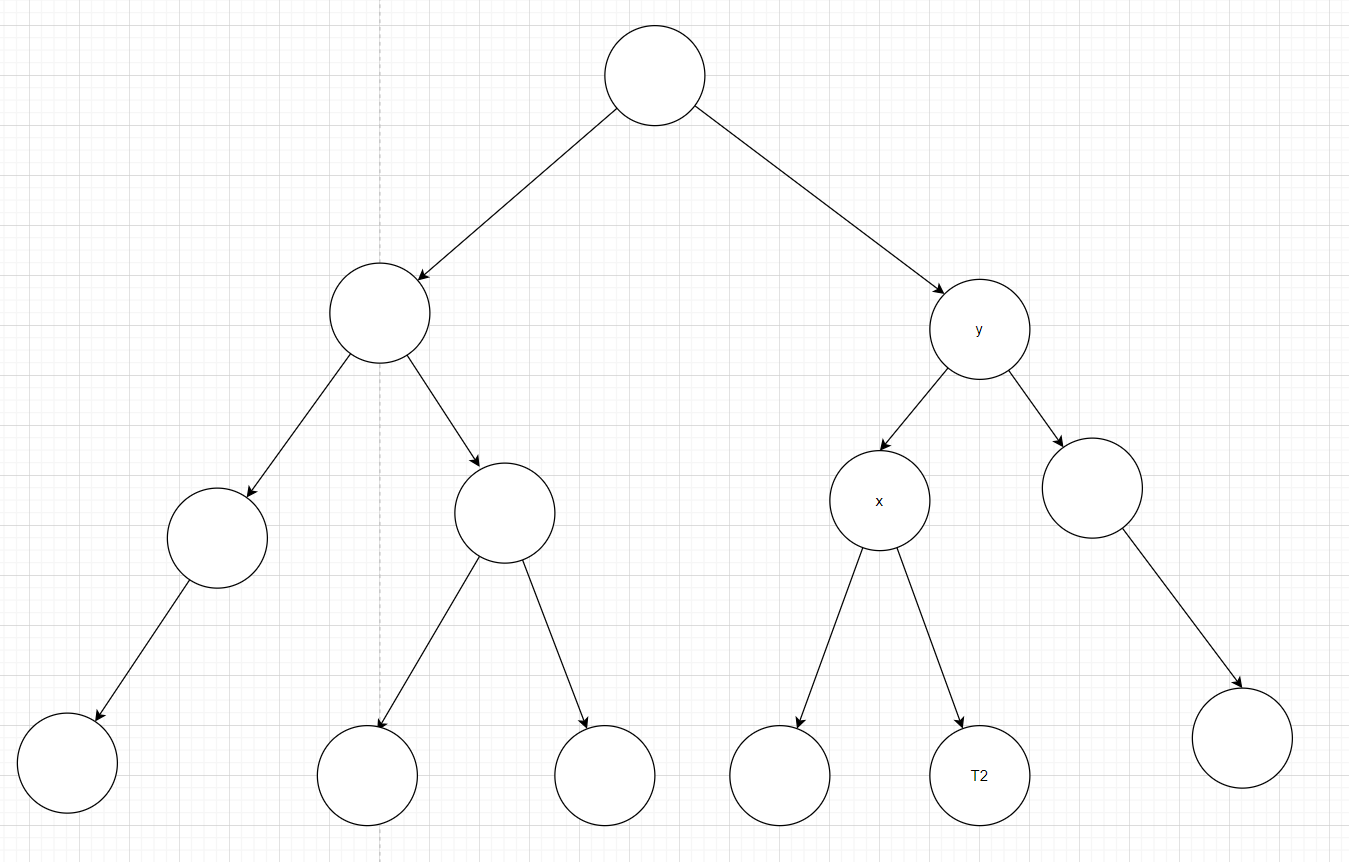
假设从图 1 变成了图 6:
图 6:
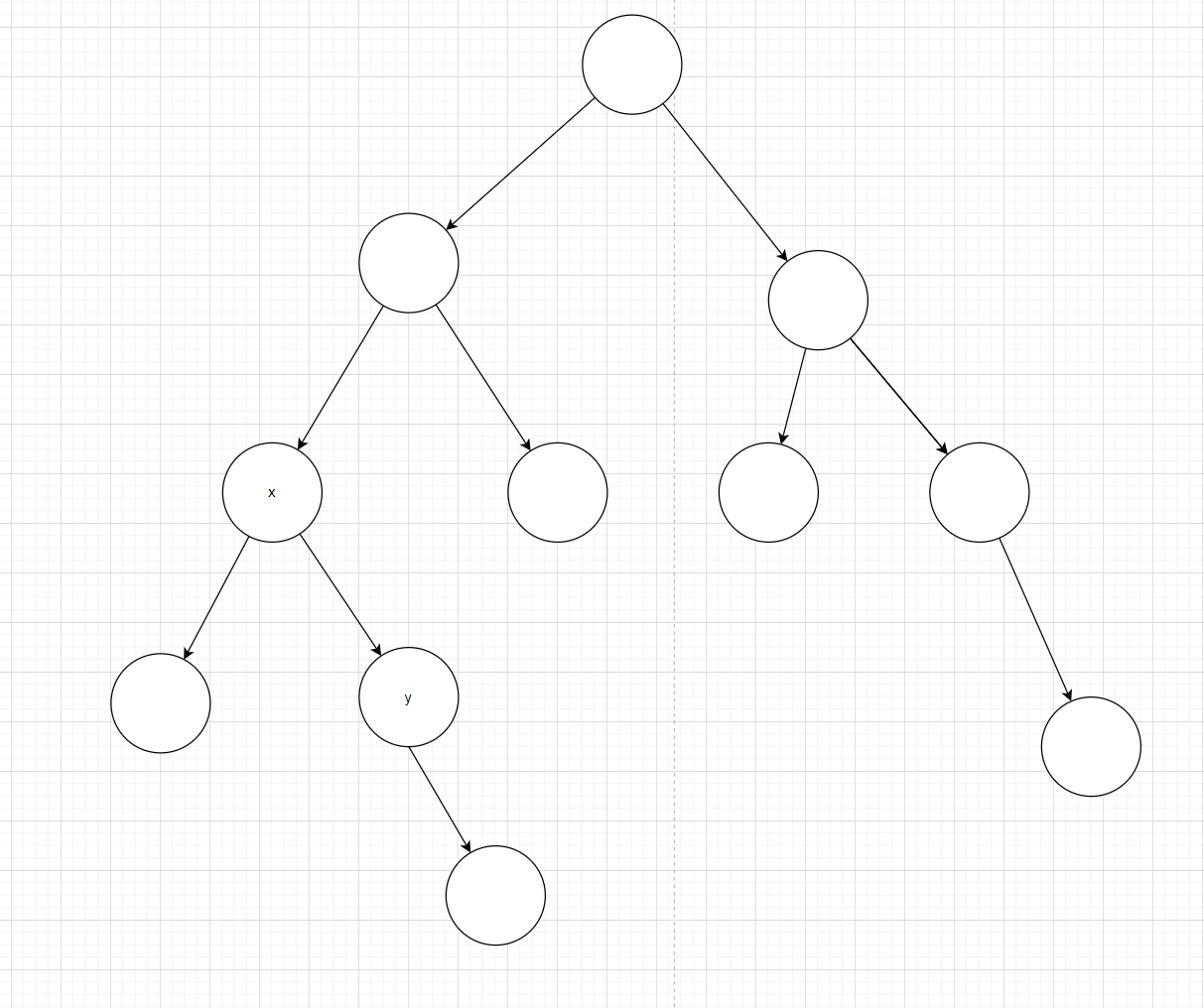
此时就是 LR,需要先进进行一次左旋
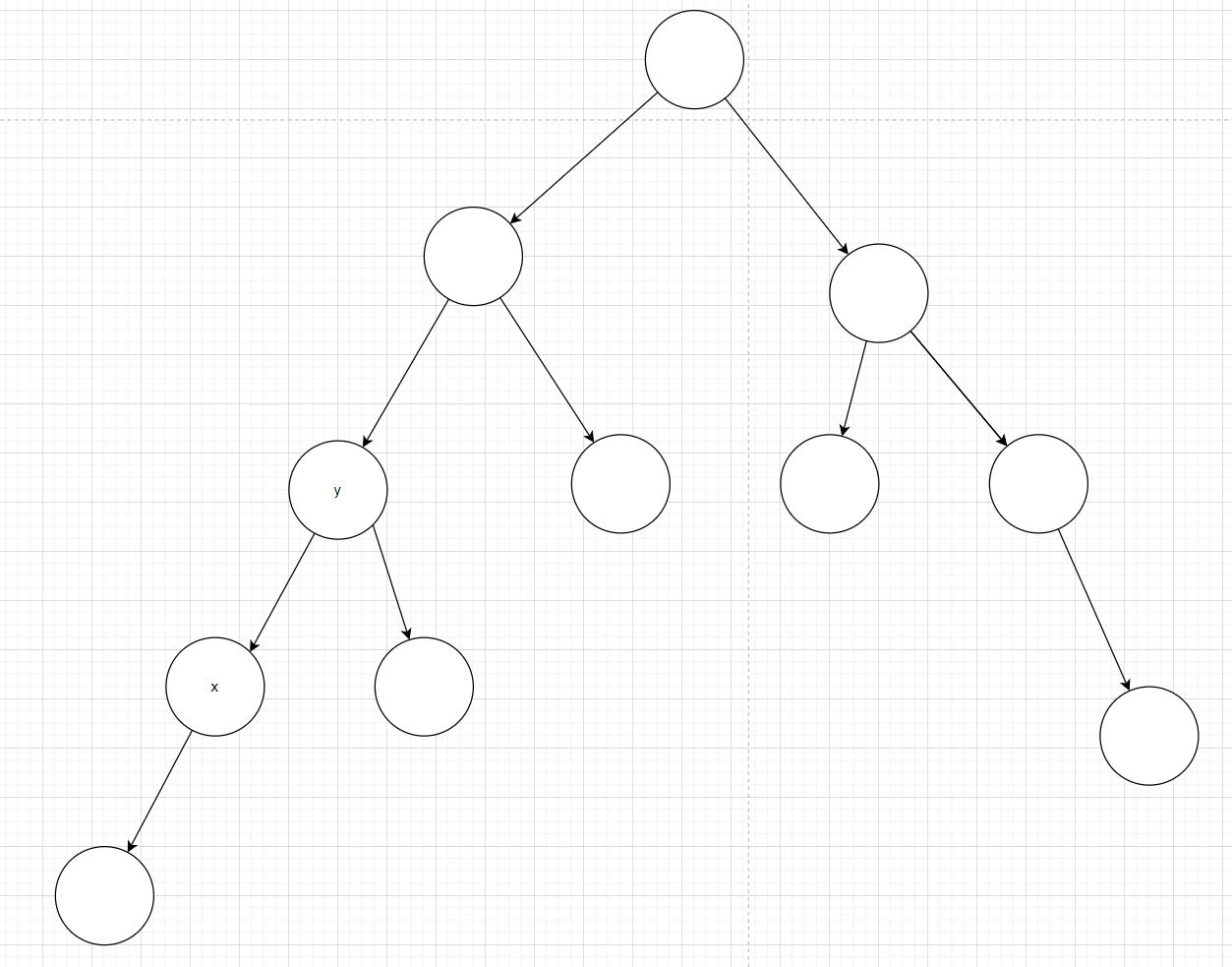
可以看到变成图 2 了,再进行一次右旋,就变成图 3 了,从图 6 到图 3 ,可以看到 LR 先左旋再右旋的变换过程其实就是把节点搬到别的地方,在保证左子树和右子树的大小的情况下,尽量保证让整个树的高度最低。
对左旋函数和右旋函数的理解
参考上面的图形和代码,应该能对左旋右旋操作有一个明确的理解了。
我们在编写函数的时候,不管是左旋还是右旋,都存在三种类型的节点,他们的关系始终是 y > T2 > x ,始终记住这个关系,写左旋或者右旋就不会乱
因为 y 是最大的节点,所以在写左旋的时候,根节点(左旋函数的参数)的是 y ,x 是 y 的左子树,同时 T2 是 x 的右子树
而写右旋的时候,x 是跟节点(右旋函数的参数),y 是 x 的右子树,T2 是 y 的左子树
旋转的作用是什么?
我们会发现,旋转之前的关系是 y>T2>x,旋转之后的关系依然是 y>T2>x,但是树的高度却降低了,
这就是旋转最神奇的地方,我们减少了子树的高度,但是我们的组织元素的方式依然是符合规则的
这个规则我们一定要保证,因为只有保证了规则,才能进行快速的二分查找,而我们进行各种旋转,都是为了降低树高,减少查找时分叉的次数
其实 T2 不是我们要修改的节点,我们也没有修改 T2,只是因为我们左旋或者右旋的时候,我们会改变 x 和 y 的指针,那之前指向的树我们不能丢掉啊,这个我们不能丢掉的子树,就是 T2 子树,
这个命名
T2是源于很多 AVL 教科书中对这种“中间子树”的惯称(有时还有T1,T3)。
其实严格来说,我们修改了 x 和 y 的左指针和有指针而已,(通过简单修改指针就能调整树高,而且保证左中右的节点的顺序,确实非常地巧妙)
我们修改了 x 和 y 的子节点,我们就得更新 x 和 y 的树高。我们没有修改 T2,所以不更新它
更新 height 的时候,一定要注意,要先更新下级节点的高度,再更新上级节点的高度,因为上级节点的高度取决于下级节点的高度
右旋之后,x 是新的根节点,y 是 x 的子节点,因此先更新 y 的高度,再更新 x 的高度,
左旋之后,y 是新的根节点,x 是 y 的子节点,因此先更新 x 的高度,再更新 y 的高度,